孙一凡

研究目的：基本概率指派的质量直接影响着决策的效果，因此如何生成高质量基本概率指派是不确定性建模的重要问题。

研究动机：数据所代表的信息通常被直接使用，而这部分信息的对立面所表示的信息却被忽视。虽然逆运算可以得到对立面的信息，但是现有的逆运算方法只能用于概率分布。

主要创新：本研究借助逆运算方法得到已有数据的反面信息，并且在进行建模时充分考虑不同子集的信息特性。

研究方法(实验步骤)：在确定辨识框架后，将概率分布的反面信息以不同的权重参数分配给辨识框架的幂集分布下的各个子集，最后聚合各个子集分配到的信息并通过归一化生成基本概率指派。

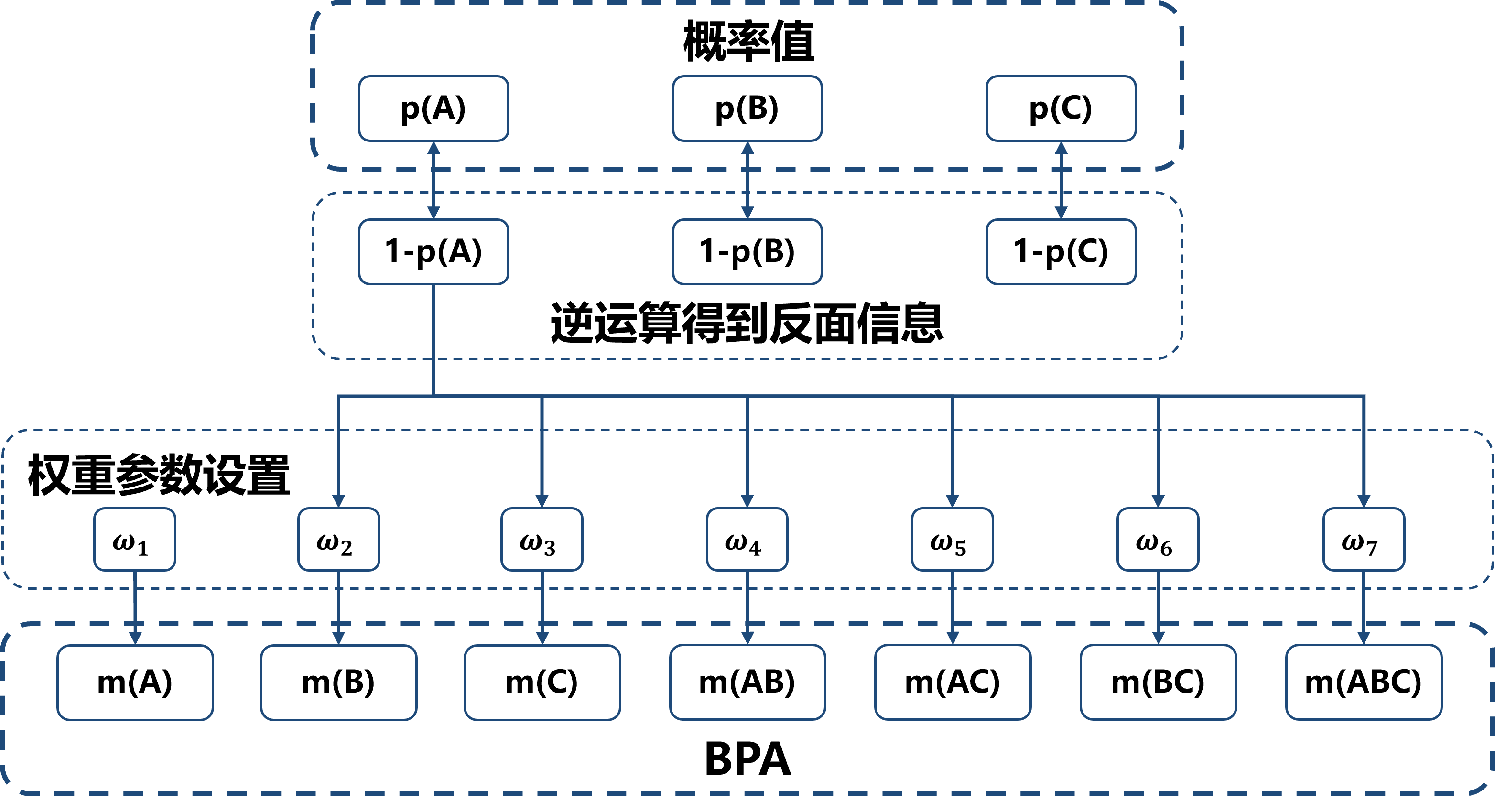
实验结果：相较于概率方法，提出的方法在iris数据集和wine数据集上的分类正确率分别提高了1.3%和1.6%(取前50组划分的平均值)，而且数据不确定性越大，提出方法的优势越明显。

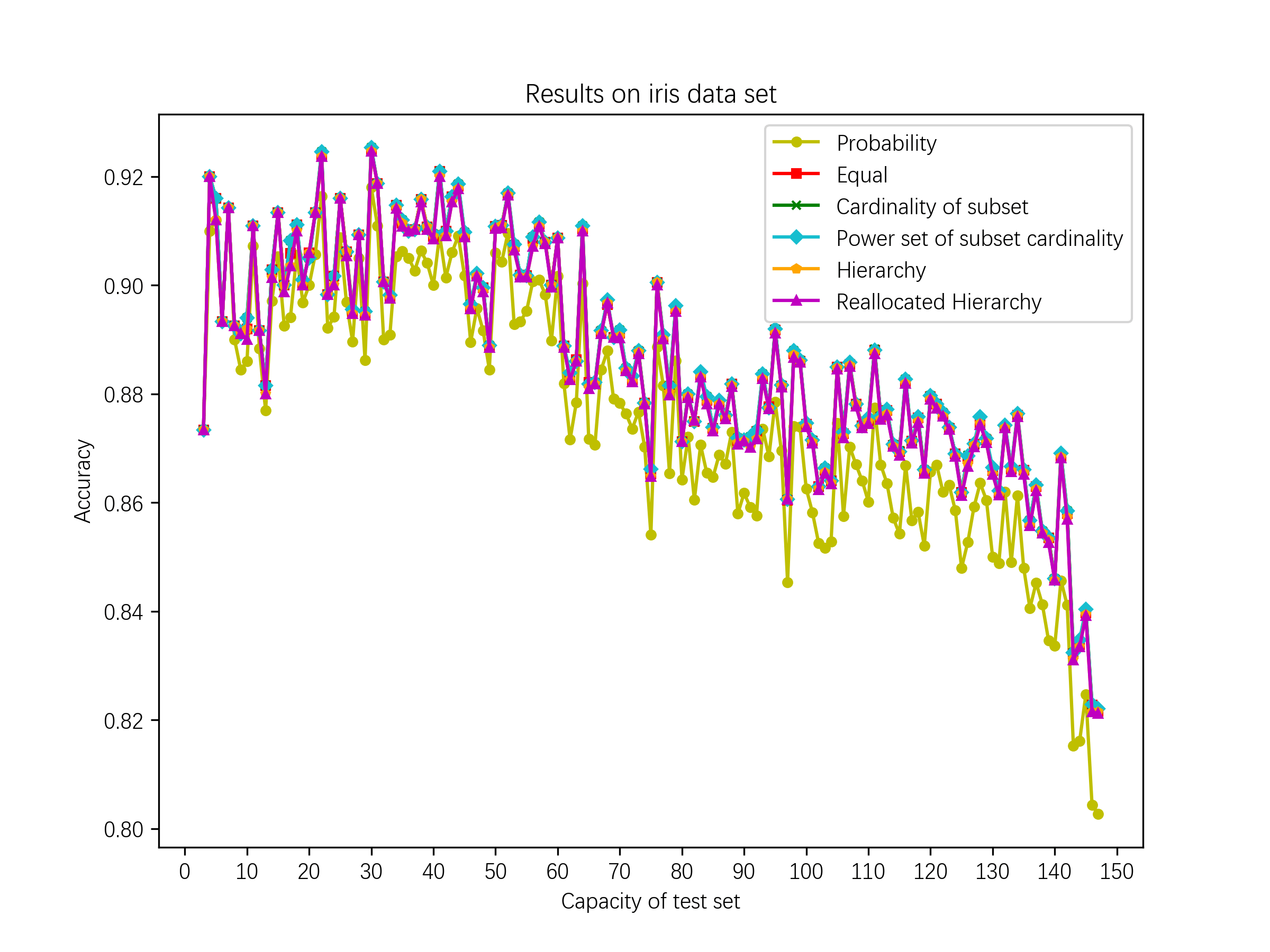
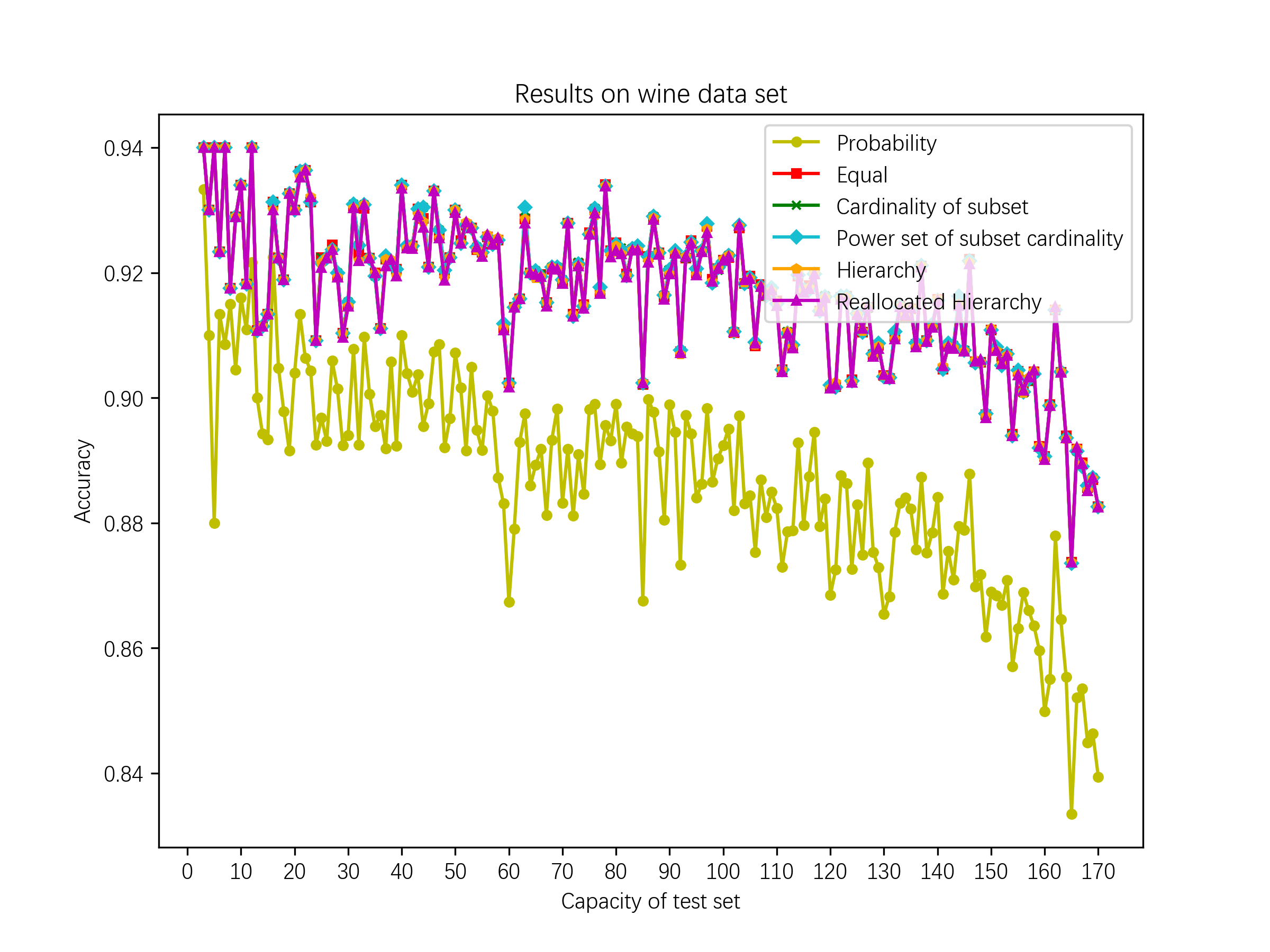
原因分析： 【不确定性表达与冲突处理】1.BPA支持集合级不确定性，允许对复合命题分配概率，显式表达“未知”，避免强行分配概率。Dempster组合规则可合并不同来源的BPA，实现更灵活的冲突处理。

成果产出：以第一作者身份投稿中科院三区期刊Computational and Applied Mathematics。

研究目的：探究不确定性度量指标的选取对证据决策树分类效果的影响。

研究动机：由于无法显式表达未知，传统决策树对不确定信息的处理会损失分类正确率。已有研究表明证据理论相关概念结合决策树模型能提高其在分类问题上的表现。然而，如何构建优秀的证据决策树是其推广应用中的重要难题。

主要创新：本研究实现了基于不同距离度量方法的基本概率指派生成模型，用多种不确定性度量指标以控制证据决策树的分支并且比较其与传统决策树在分类任务上的表现差异。

实验结果：

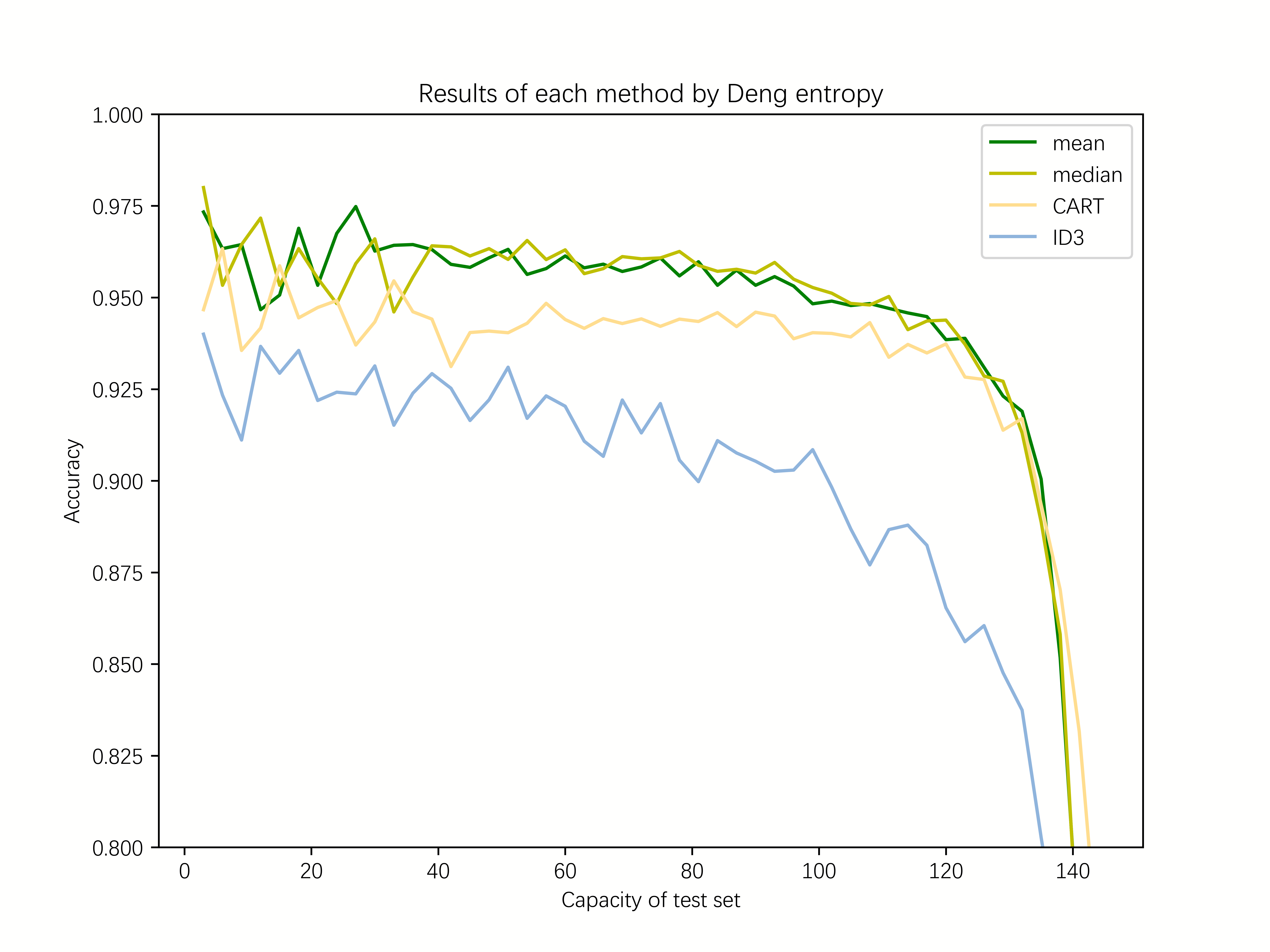
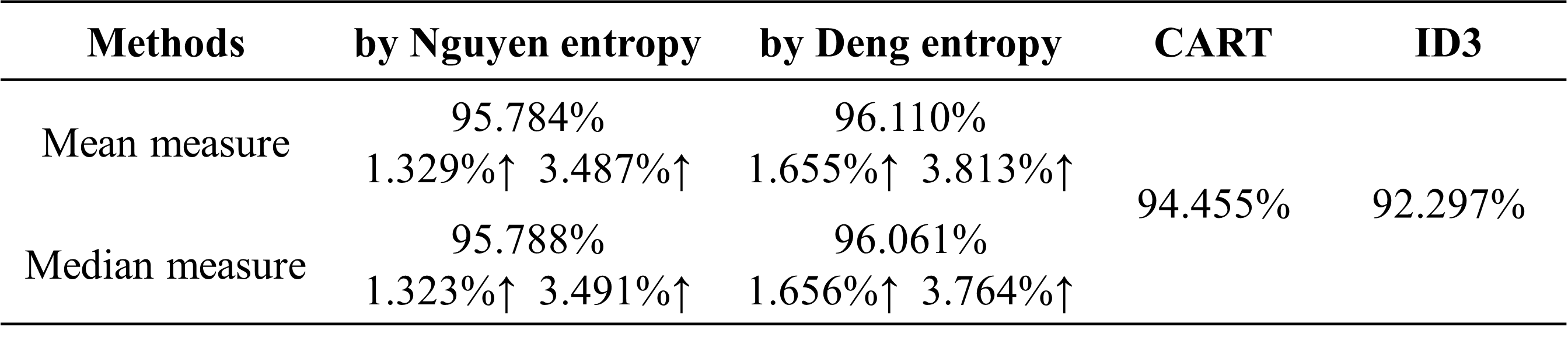
• 1.与传统决策树方法相比，选择的两种熵值方法在iris数据集上的分类正确率分别提高了1.3%和1.6%(取前25组划分的平均值)。

• 2.Deng熵的表现比Nguyen熵更好。

• 3.不同的距离度量对结果影响较小。

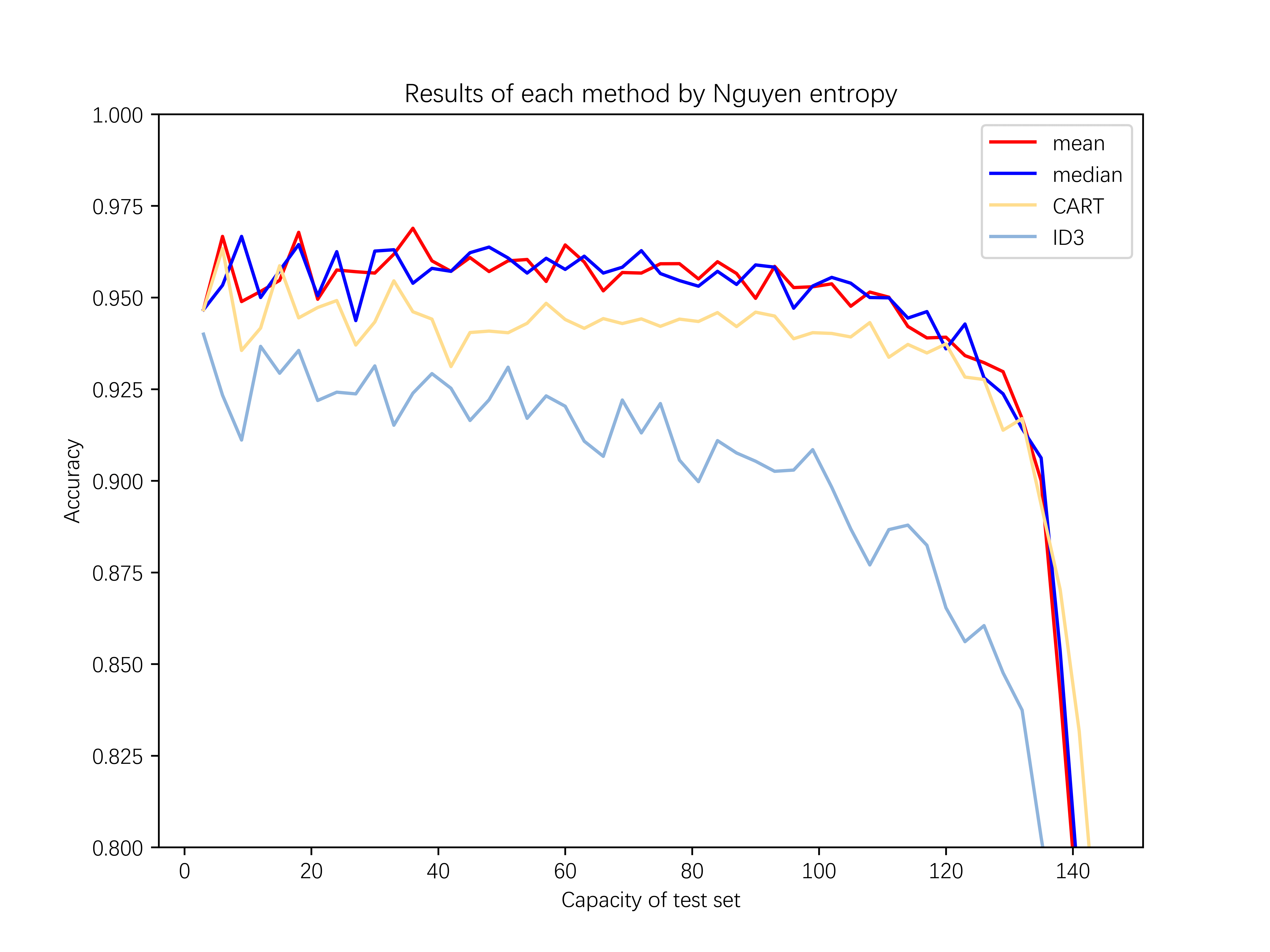
原因分析：

• 1.【对决策树的作用机理】证据理论领域的熵值能有效地度量不确定性，从而保证分割属性按信息含量的降序排列。同时，多个区间的使用保证数据被更合理地划分。

• 2.【熵值特性】Deng熵考虑幂集基数，能更好衡量不确定性的粒度。对非单子集(如{A,B})赋予更高不确定性，更符合DST的初衷。而Nguyen熵是基于BPA的Shannon熵扩展。它仅依赖BPA值，忽略幂集结构，可能低估冲突证据的不确定性。

• 3.【距离性质】这两种距离度量对测试样本与训练样本之间差异性的量化能力相近。也可能与数据分布有关。

成果产出：以第一作者身份在EI会议2024 7th International Conference on Algorithms, Computing and Artificial Intelligence(ACAI 2024)上发表论文，论文已经被EI检索。论文链接 查看全文 查看会议论文集

研究背景：证据理论的可靠性假设认为所有信源的可靠性都相同，这会对使用Dempster正交和法则的融合结果的准确率会产生消极影响，从而限制证据理论在信息融合领域的进一步应用。

研究动机：复数证据理论的提出证明了从实平面向复平面的变换能提高融合效果，突破了可靠性假设的制约。散度测量可以量化信度函数之间差异，进而反映证据体之间的冲突程度。散度可以量化不同来源信息间的差异性，但是已有的散度测量方法尚不能很好地处理复数场景下的问题。因此，如何在复数空间中建立能有效测量散度的方法仍是亟待解决的问题。

主要创新：将Kullback-Leibler散度中使用的质量函数拓展成复数质量函数(CM)，进而将信念Jensen-Shannon散度(BJ-SD)拓展成复数信念Jensen-Shannon散度(CVBJ-SD)。相较于原本方法，该散度测量方法具有非负性、对称性、自反性和传递性等优秀特性。

研究方法(实验步骤)：在确定辨识框架后，计算出其幂集分布下各子集所含样本在添加测试集样本前后的标准差和均值的变化量以生成复数质量函数。接下来计算出其对应的CVBJ-SD矩阵【因为散度衡量了不同属性间的差异，当某属性与其他属性的差异过大时，即可认为该属性可靠性低，于是为其分配更小的权重】，将某属性的散度处理后用作原复数质量函数的权重系数，得到该属性的加权平均证据。最后根据Dempster正交和法则两两融合属性得到最终的加权平均证据【因为Dempster没能区分不同信源的可靠性，所以这里沿用是为了融合(乘到一起)】。

实验结果：与原始的融合方法相比，提出的方法在iris数据集、wine数据集和seed数据集上的分类准确率分别提高0.27%、27.2%和0.21%。并且数据的不确定性越大优势越显著。

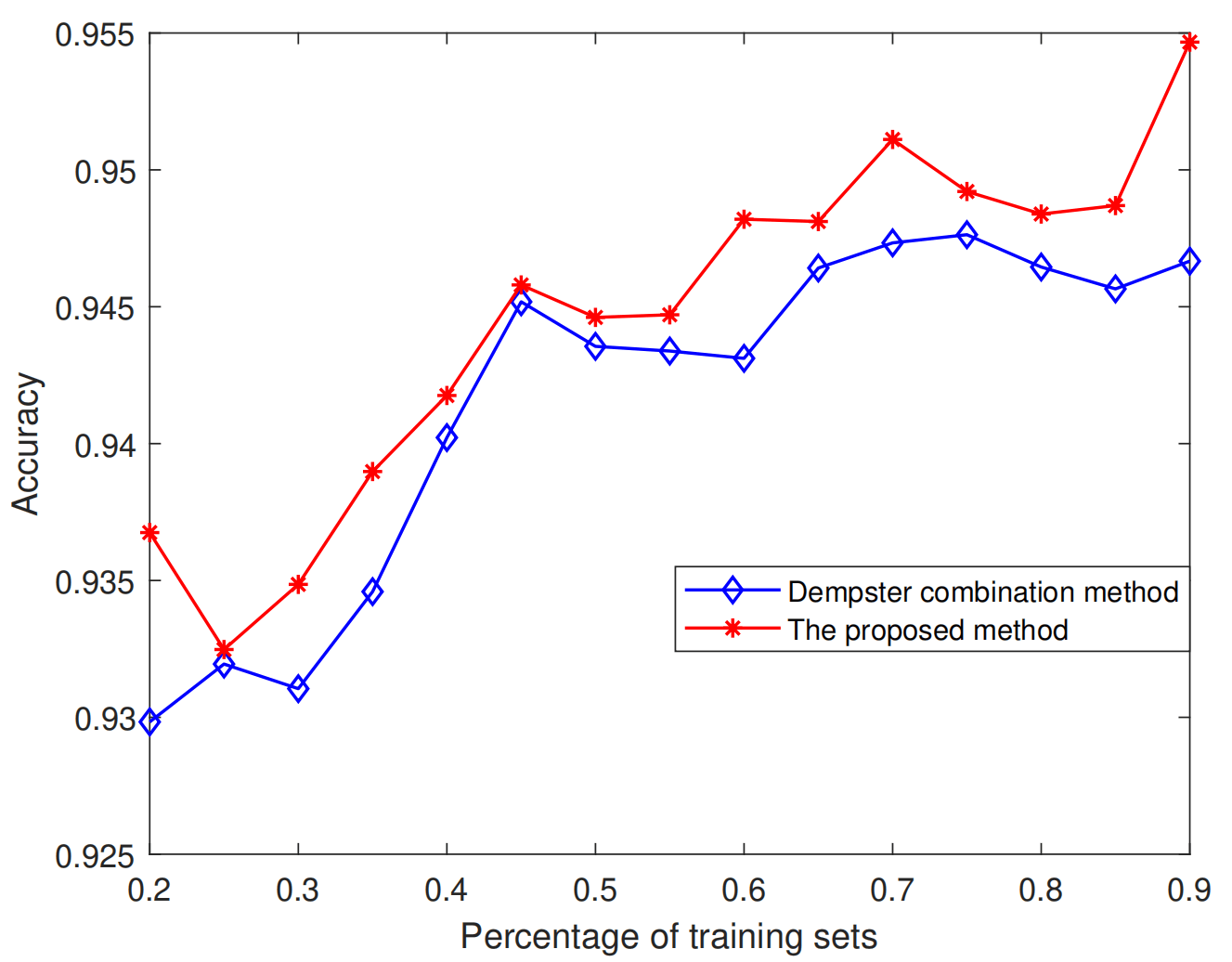
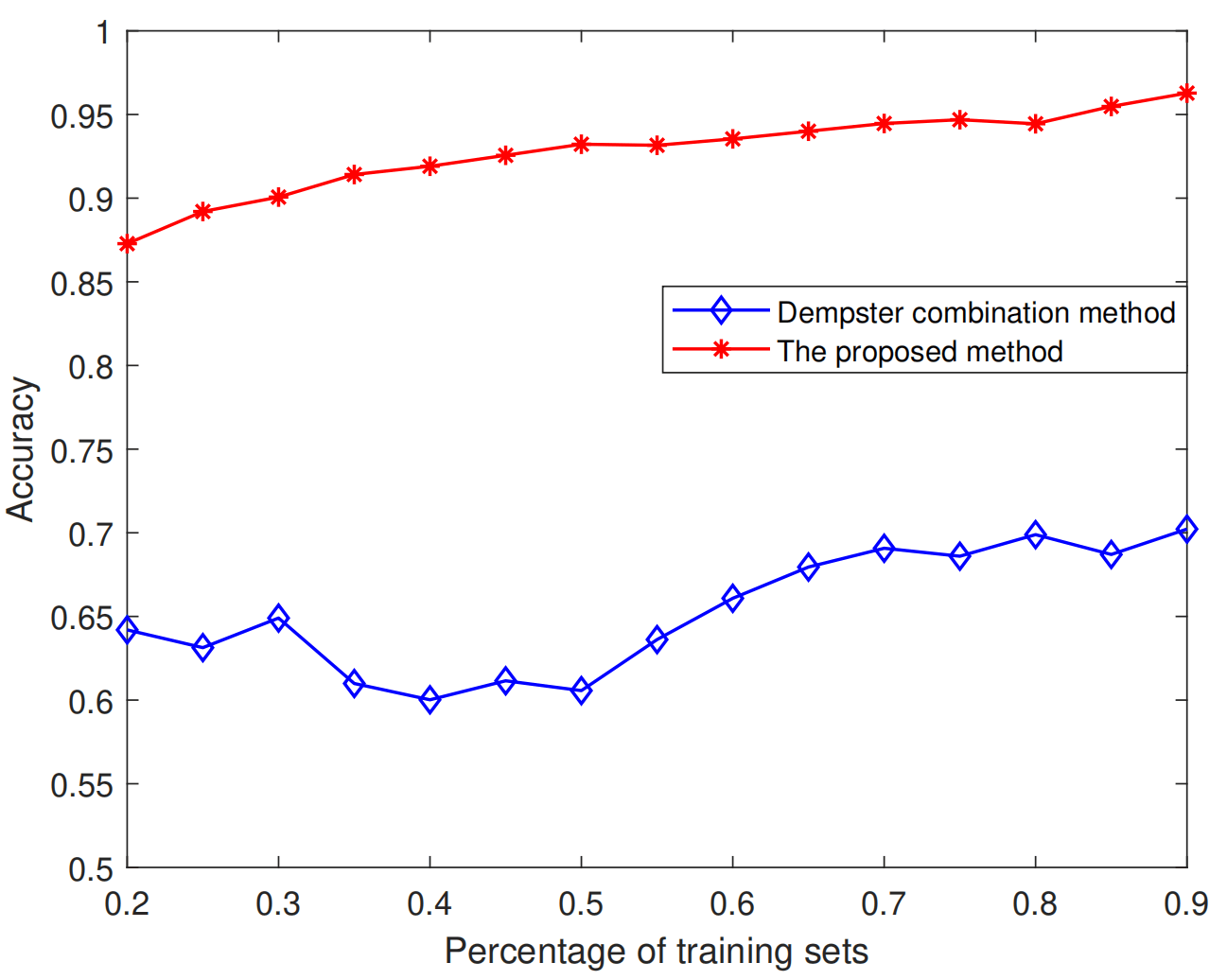
原因分析：

• 1.【表达能力】复数证据理论通过引入振幅和相位，更好地表达置信度大小和信息冲突类型，能实现对不确定性信息更准确的建模。

• 2.【融合能力】Dempster规则在高冲突证据下可能产生反直觉结果（如Zadeh悖例），而复数证据理论通过调整相位，可区分冲突是源于噪声(相位随机变化)还是本质矛盾(相位持续相反)，对噪声更鲁棒（相位信息可过滤部分噪声）。

• 3.同时复数组合规则能避免过度归一化，保留更多信息，提供更精准的冲突管理，从而提高信息融合效果。

成果产出：以第二作者身份在期刊Computational and Applied Mathematics上发表论文。论文链接

启发来源：阅读论文《Deep evidential fusion with uncertainty quantification and reliability learning for multimodal medical image segmentation》。原文链接

提出的框架：（特征提取模块->证据映射模块->多模态证据融合模块）

特征提取模块：使用医学图像分割领域经典模型Unet。

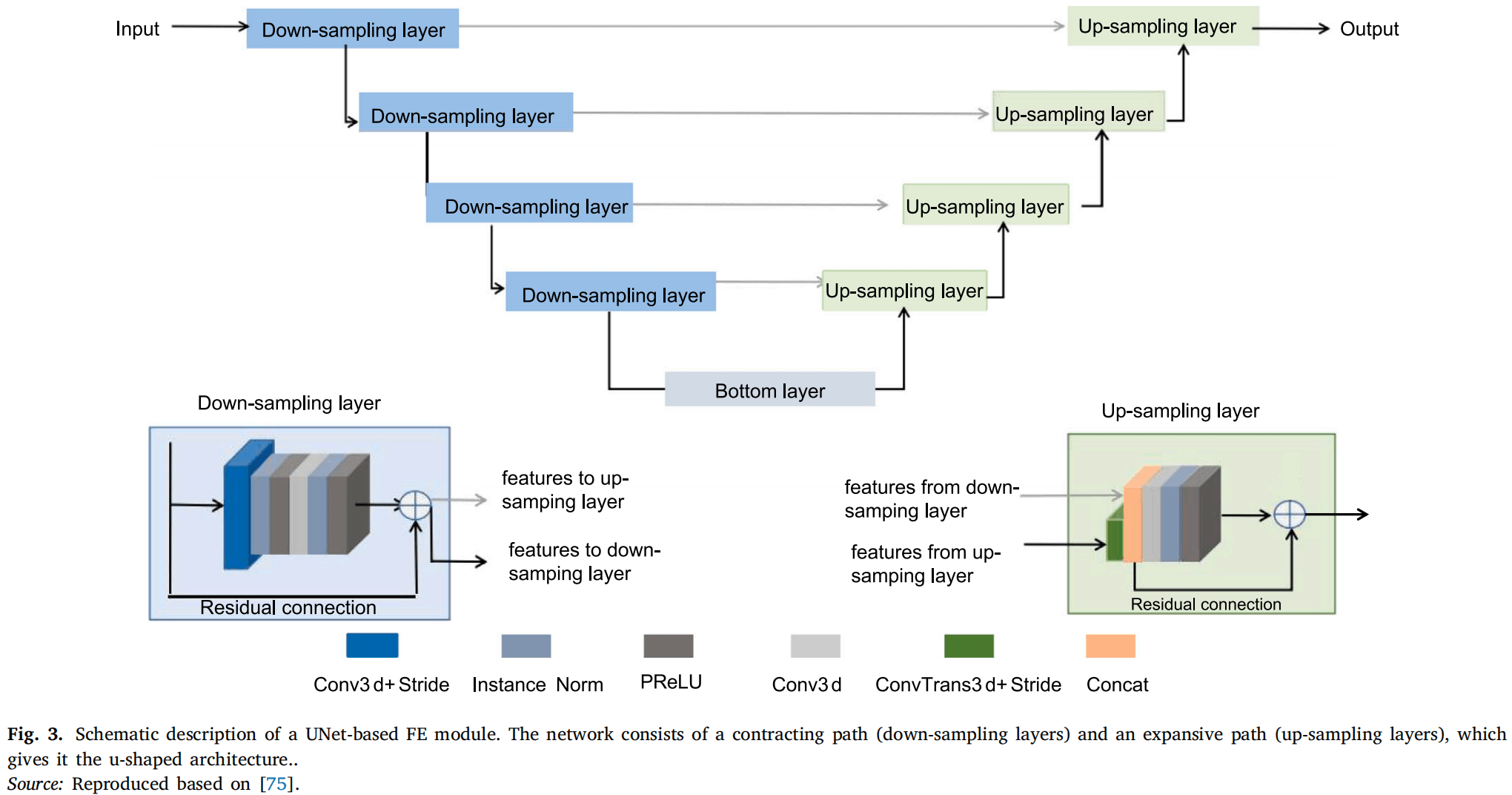
证据映射模块：

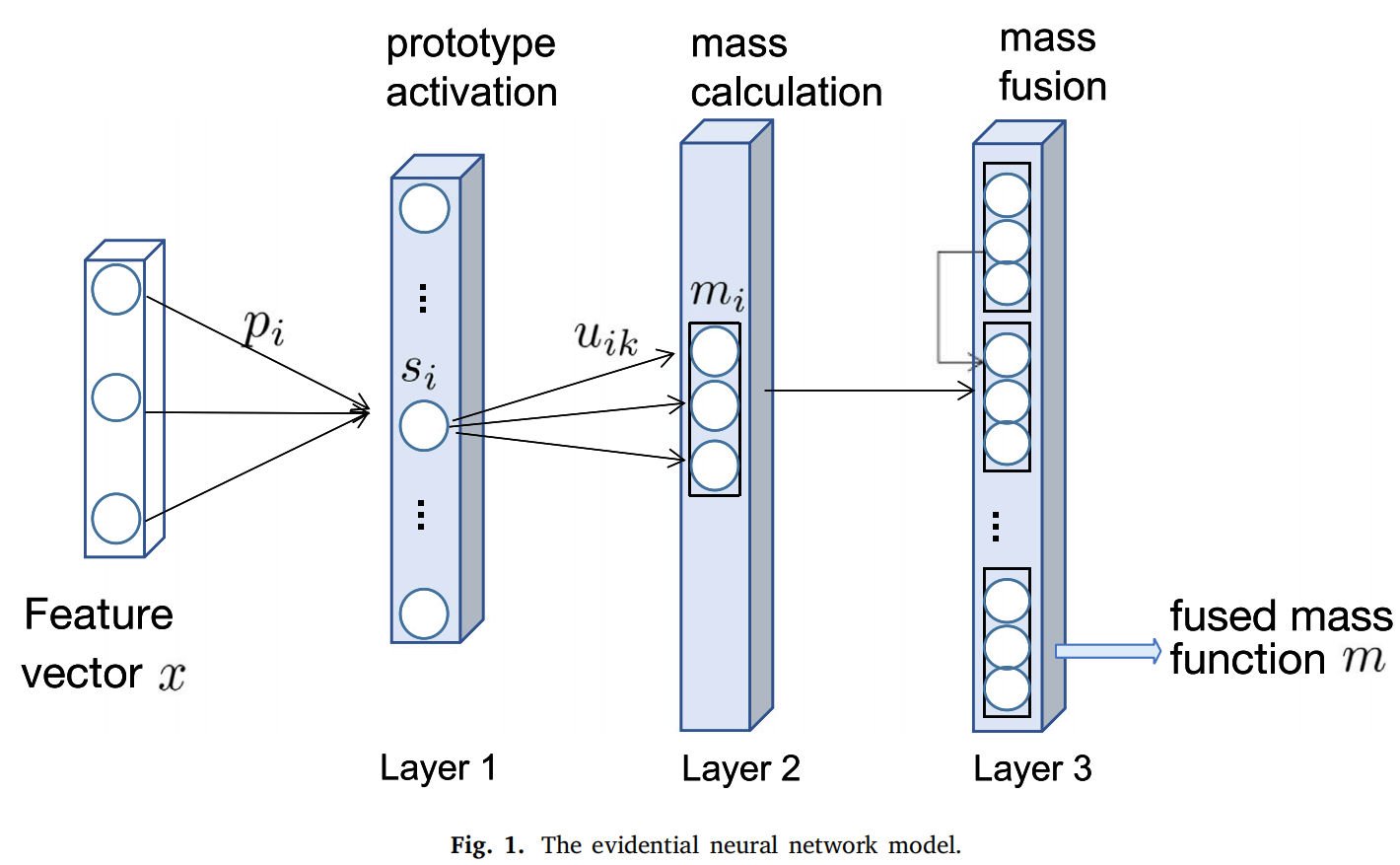
• （原型激活层）将提取出的特征与原型特征输入特征激活层，得到激活函数值。

• （质量计算层）将该函数值按照由学习得到的隶属度分配给类别的单子集，将1-函数值分配给类别的全集。

• （质量融合层）按照Dempster正交和规则将上一层得到的质量函数两两融合，输出最终经过融合的质量函数。

多模态证据融合模块：将每个模态输出的融合后的质量函数进行上下文折扣操作，为各个模态学习到适合其的可靠性因子，最后将经过折扣的轮廓函数按照似真概率转换得到输出类别的概率值。

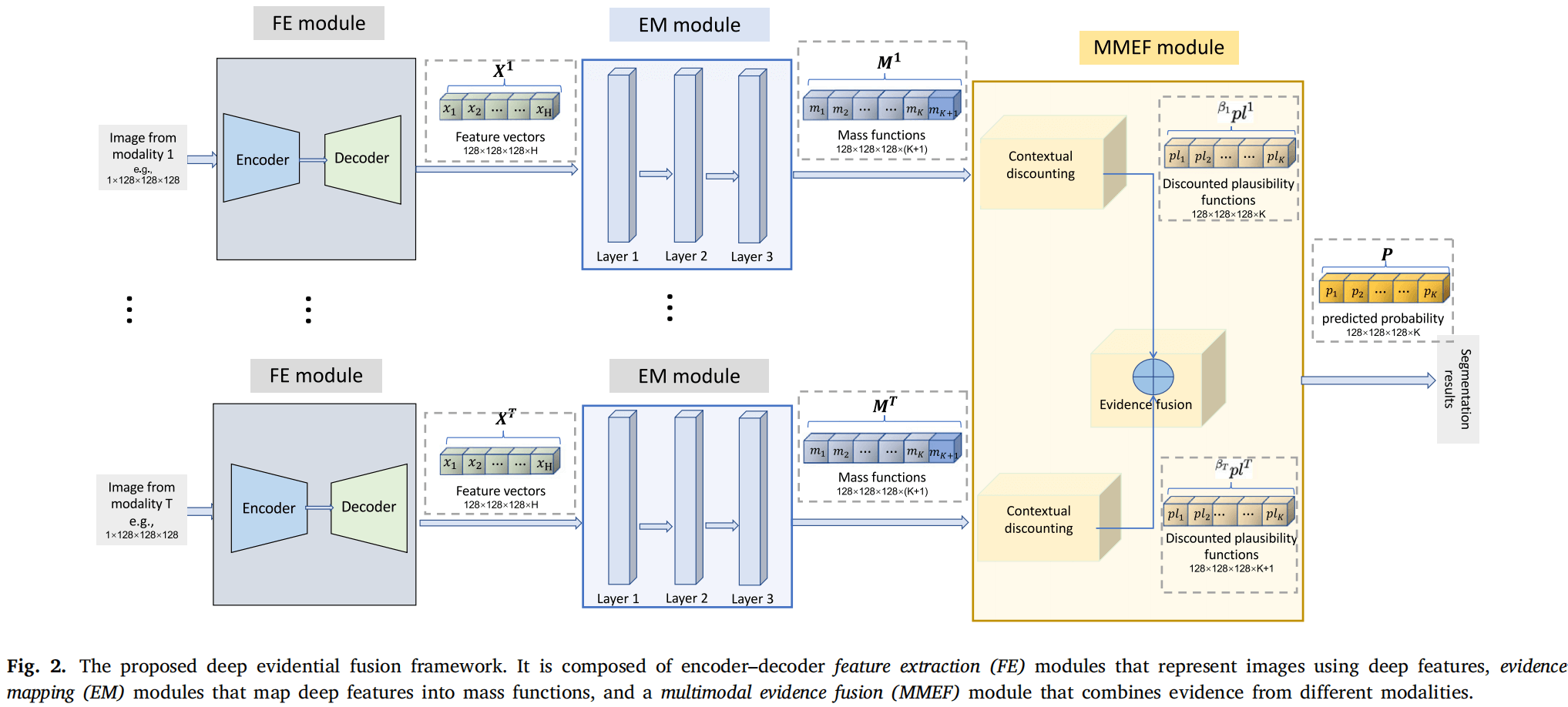
损失函数：平衡各模态独立的分割表现与融合之后的分割表现。

可能的改进：

• 1.使用全部的质量函数以辅助更精确的决策，而不是仅使用轮廓函数。

• 2.使用其他的质量函数修正方法，而不是上下文折扣操作。